3. 简单DP:斐波那契数

发布时间: 2018-09-30 15:23:37.0 点击: 266
以下序列为斐波那契数列: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... 即满足F(n) = F(n-1)+F(n-2),其中F(0) = 0, F(1) = 1。 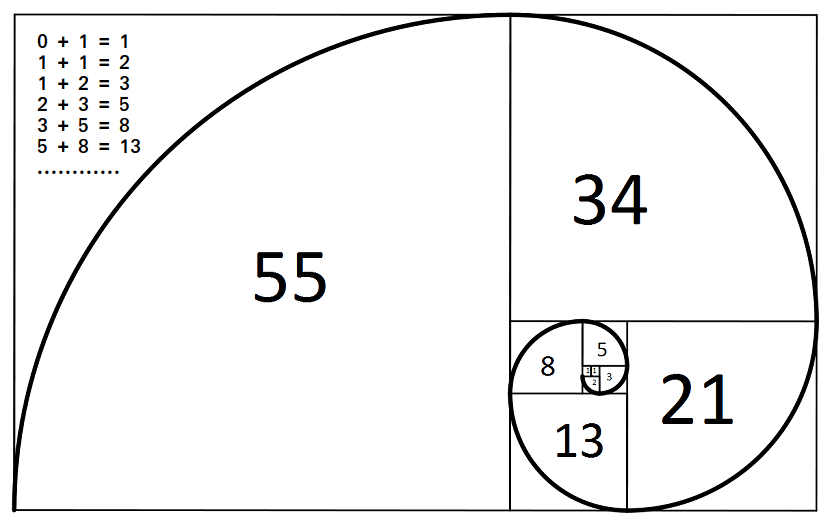
方法一:递归 如果n为0或1,返回n,否则进行递归调用返回F(n-1)+F(n-2)。 int fib(int n) { if (n <= 1) return n; return fib(n-1) + fib(n-2); } |
时间复杂度为指数增长,约O(2^N),因为有很多重复子问题(前文已有描述),空间复杂度:如果考虑栈开销为O(n),否则O(1)。 方法二:动态规划 int fib(int n) { int f[10000];//n<10000 int i; f[0] = 0; f[1] = 1; for (i = 2; i <= n; i++) { f[i] = f[i-1] + f[i-2]; } return f[n]; } |
可以将中间结果保存(记忆化或造表),时间和空间复杂度均为O(n): 方法三:空间优化(适合于只求一次) 只保存前面两个值,滚动计算后面的斐波那契数,时间复杂度O(n),空间O(1)。 int fib(int n) { if(n<2) return n; int a = 0, b = 1, c, i; for (i = 2; i <= n; i++) { c = a + b; a = b; b = c; } return b; } |
方法四:快速矩阵幂 将斐波那契推导公式转化为矩阵: 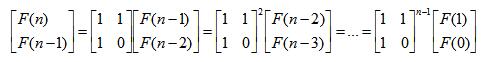
根据快速矩阵幂,可以更高的效率计算出斐波那契数。 因为F(1)=1,F(0)等于0,因此矩阵: 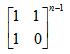
的最左上角即为F(n),时间复杂度O(Log2N)。 void multiply(int F[2][2], int M[2][2])//两矩阵相乘 { int x = F[0][0]*M[0][0] + F[0][1]*M[1][0]; int y = F[0][0]*M[0][1] + F[0][1]*M[1][1]; int z = F[1][0]*M[0][0] + F[1][1]*M[1][0]; int w = F[1][0]*M[0][1] + F[1][1]*M[1][1]; F[0][0] = x; F[0][1] = y; F[1][0] = z; F[1][1] = w; } //暴力速度慢 void power(int F[2][2], int n) { int i; int M[2][2] = {{1,1},{1,0}}; for (i = 2; i <= n; i++) multiply(F, M); } //快速幂 void fastpower(int F[2][2], int n) { if( n == 0 || n == 1) return; int M[2][2] = {{1,1},{1,0}}; fastpower(F, n/2); multiply(F, F); if (n%2 != 0) multiply(F, M); } int fib(int n) { int F[2][2] = {{1,1},{1,0}}; if (n == 0) return 0; fastpower(F, n-1); return F[0][0]; } |
|
|
