动态规划用于解决一类复杂问题，它将问题分解为子问题进行求解先，并存储子问题结果以避免反复求解。一般具有以下两个重要性质的问题都可以通过动态规划求解：

（1）重叠子问题：类似分治法，动态规划也是利用子问题进行求解，如果很多子问题需要反复求解，那么存储起来就可以避免重复计算，但如果没有重叠子问题，动态规划就失去意义。比如在二分查找中，各个子问题彼此不重叠，不需要动态规划。但在求斐波那契数时，很多子问题需要反复计算：

int fib(int n)

{

   if ( n <= 1 )

      return n;

   return fib(n-1) + fib(n-2);

}

比如在求解fib(5)时，fib(3)需要调用2次，最好存储起来避免反复调用。

有两种方法用来存储中间变量，分别是造表和记忆化。

（2）最优子结构：即问题的最优解可以通过各个子问题中求最优解得到，这种性质称为最优子结构。比如在求解最短路径时，如果x位于从顶点u到顶点v的最短路径上，那么这条最短路径必然是从u到x的最短路径和从x到v的最短路径组合而成。其中Floyd-Warshall和Bellman-Ford算法都是典型例子。

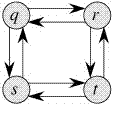
反过来，求最长路径（不含回路）就不满足最优子结构性质，比如在下图中，从q到t的最长路径有两条：q->r->t和q->s->t，其中第一条它不是q到r的最长路径（q->s->t->r）和r到t的最长路径（r->q->s->t）组成的。

（3）造表VS记忆化

在求解动态规划过程中，为了存储计算过的中间值（为了重用），有两个方法：造表（自底向上）和记忆化（自顶向下）。

在状态转换时，如果我们以dp[0]为基础推导出dp[x]，再推导出dp[x+1]，最终求得我们的目标dp[n]，我们就称之为自底向上。比如当我们求解斐波那契数列时：

// 造表求斐波那契数列

int dp[MAXN];

int dp[0] = 1;//基础状态

for (int i = 1; i< =n; i++)

{

    dp[i] = dp[i-1] * i;

}

这里的状态转换是线性的，因此只要一维存储。

如果，我们在求dp[n]时，不是从基础状态（如dp[0]）推导，而是去寻求能够产生dp[n]的前导状态，那么这种方法就称为自顶向下的。

// 为了提高效率，存储中间值（-1表示未求过），记忆化求斐波那契数列，

int dp[MAXN]

int solve(int x)

{

    if (x==0)

        return 1;

    if (dp[x]!=-1)

        return dp[x];

    return (dp[x] = x * solve(x-1));

}

同样，这里记忆的变量是一维数组，今后会碰到二维情况。

最后总结一下它们的特点：

（4）如何求解动态规划问题

根据动态规划的两个性质，步骤如下：

1）确定是否是动态规划问题：一般求最小值或最大值或者计数这些问题可能会是动态规划问题，再检查子问题是否重叠，是否满足最优子结构性质，如果满足一般就是动态规划问题。

2）使用最少的参数来定义状态：DP的主要步骤就是状态的变换，因此状态定义很关键，状态用来表达问题中间某种值，参数要尽可能少以用来节省状态空间。比如在求解背包问题时，使用索引（index）和背包容量（weight）两个参数来定义状态DP[index][weight]，即最优解可以通过第0到index之间容量为weight的不同值得到。

3）使用公式表示状态之间的关系：这是相对来说是最为复杂的一步，需要多加观察和实践。举个例子：

使用动态规划进行思考：首先我们使用参数n来确定一个状态，表示为state(n)，即state(n)是指使用{1, 3, 5}来分解n的方法数。接下来要思考状态之间的关系，假设我们已经求得了n=1,2,3,4,5,6时的状态即state(n=1)、state(n=2)、state(n=3)...state(n=6)，考虑求解state(n=7)，因为我们只能添加1、3和5，因此我们分三种方法添加：

1) 在state (n = 6)基础上加1
Eg : [ (1+1+1+1+1+1) + 1]
[ (1+1+1+3) + 1]
[ (1+1+3+1) + 1]
[ (1+3+1+1) + 1]
[ (3+1+1+1) + 1]
[ (3+3) + 1]
[ (1+5) + 1]
[ (5+1) + 1]

2) 在state (n = 4)基础上加3;

Eg : [(1+1+1+1) + 3]
[(1+3) + 3]
[(3+1) + 3]

3) 在state(n = 2)基础上加5
Eg : [ (1+1) + 5]

以上已经全部覆盖了和为7的情况，因此得到状态之间关系：

state(7) = state (6) + state (4) + state (2)
或
state(7) = state (7-1) + state (7-3) + state (7-5)

推广到n的情况则：
state(n) = state(n-1) + state(n-3) + state(n-5)

递归的代码如下：

int solve(int n)

{

   if (n < 0)

      return 0;

   if (n == 0)  

      return 1;  

   return solve(n-1) + solve(n-3) + solve(n-5);

}

4）造表或者记忆化

上述递归代码很容易改造成记忆化（你也可以自行通过造表进行递推解决）：

int dp[MAXN];//需要事先初始化为-1

int solve(int n)

{

  if (n < 0)  

      return 0;

  if (n == 0)  

      return 1;

   if (dp[n]!=-1) //检查是否已经求解

      return dp[n];

    return dp[n] = solve(n-1) + solve(n-3) + solve(n-5);// 存储结果并返回

}