用一个数组rel[]存储当前结点a 与 父节点fa 的关系
0: 同类
1: fa 吃 a
2: a 吃 fa
把能确定关系的结点都合并在同一个集合里,而不是把同类的放在同一个集合里。
对任意两个元素 x 与 y ,和 关系 D
Fx=Find(x ); Fy = Find(y );
若Fx == Fy 说明能确定x 与 y 的 关系 ,如图,向量xy=(rel[y]-rel[x]+3)%3 即,x到 y 的关系D-1因满足 等式右边的条件,若不满足,就是假话
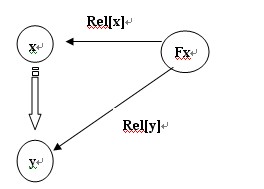
若Fx != Fy 就要合并
Ani[fy]=fx;
rel[Fy]=(rel[x]+d-1- rel[y]+3)%3 该公式同样是由向量的运算来的
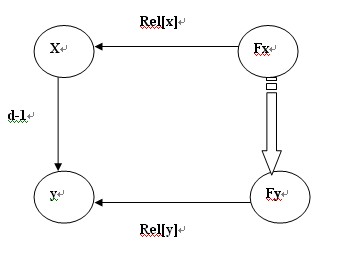
在查找一个元素x 时,要压缩路径,此时,要改变rel[x],原来是x 与 父节点 Fx 的 关系 ,现在要改成 x 与 根结点 rx 的关系,同样可以用向量图表示rel[x]=(rel[x]+rel[rx])%3
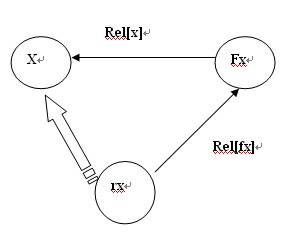
核心代码:
for(i=0;i<k;i++)
{
scanf("%d%d%d",&d,&a,&b);
if(a>n || b>n)
lie++;
else
{
fa=Find(a); fb=Find(b);
if(fa!=fb)
Merge(a,b,fa,fb,d-1);
else
{
if((rel[b]-rel[a]+3)%3!=d-1)
lie++;
}
}
}
int Find(int x)
{
int fx=ani[x];
if(x==ani[x])
return ani[x];
ani[x]=Find(ani[x]);
rel[x]=(rel[x]+rel[fx])%3;
return ani[x];
}
void Merge(int a,int b,int fa,int fb,int d)
{
ani[fb]=fa;
rel[fb]=(rel[a]+d-rel[b]+3)%3;
}
对于几个公式,一开始没明白是怎么出来的,网上说是向量偏移,整理了一下,画了几张图,希望会有帮助。 向量的知识貌似是高中的,都忘光了呢,琢磨了好久,才想起来了一点,呵呵~。因为传图片的事纠结了一小会,谢谢大家,又让我学到了新知识。谢谢...
