D:乡村医院

赶时间请从第四段开始。

此题我用的是二分，题目输出是最小的最远距离，因此二分距离，想到这点我觉得就没问题了。

初看题目，是想将m个医院分配，感觉是DP，DP需要最优子结构和子结构重叠，显然难找不科学。然后搞了半天，看到题目的输出“对每组输入数据输出一个整数，表示最小的最远距离”，就转换了个思路，从距离入手。

显然，一开始二分h=a[n-1]-a[0]，l=0，则最远距离mid=(h+l)/2，然后判断以此最远距离是否可建立小于或等于m个医院，覆盖所有村庄。

i=j=k=f=0;

while(i<n&&j<n)

{

if(k==m){f=1;break;}

while(a[i]-a[j]<=mid&&i<n)i++;

j=i-1;

while(a[i]-a[j]<=mid&&i<n)i++;

j=i;

k++;

}

f用来标记以mid为最远距离建医院是否可行，k来标记医院个数，然后顺序找距离第j个村庄最远的，满足<=mid的最远村庄i，则在i-1这个村庄位置建立一个医院（因为循环出来的时候a[i]-a[j]>mid了，所以是i-1的位置建），然后将j=i-1，向j位置(这位置上有医院)的右边顺序查找，直到找到某个最远的村庄，其距离到这个有医院的村庄最远，记录下位置j=i（此处不用i-1），然后结束一次查找，增加医院数目k++。如上建立医院，若能在k未到达医院最大上限m的情况下，完成覆盖所有村庄，说明以mid为最远距离建立医院可行，则二分查找小于mid距离的情况，h=mid-1，否则l=mid+1，如此二分查找下去，直到完毕，返回l的值,既为最小的最远距离。

以下以样例1讲解下，

5 2

0 1 2 5 6

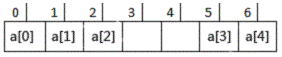
二分开始 l=0，h=a[n-1]-a[0]=6，mid=3

判断以mid为最远距离，是否可以建立<=m个医院，使所有村庄都被覆盖。

进入while(i<n&&j<n)

执行while(a[i]-a[j]<=mid&&i<n)i++;

到i=3时跳出循环，j=i-1=2; 则第一个医院在j处。

再执行while(a[i]-a[j]<=mid&&i<n)i++;

在从i=2向右找在mid最远距离内的村庄，一直找到a[4]，a[4]-a[2]>mid(6-2>3)，退出循环。

j=i;k++;  (j=i=4,k=1)

因为未覆盖完所有村庄，i<n&&j<n，所以继续。

执行while(a[i]-a[j]<=mid&&i<n)i++;

出来i==n;

退出外while循环。

此时根据f标记知道，在最远距离为mid的情况可以覆盖全部村庄，所以h=mid-1，去找比这个最远距离更小的情况，看是否有更小的最远距离。

再次二分……以下类似。

最后得到最小的最远距离。